Every good regulator of a system must be a model of that system.
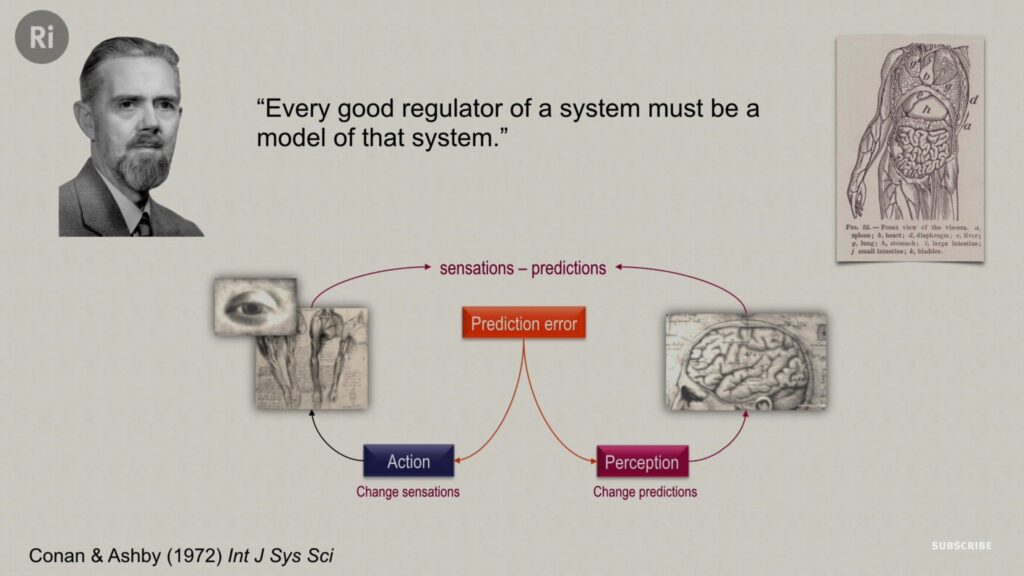
The good regulator idea applies to all real-world systems, that is, all systems that manage others or are self-regulating. An organism needs a model of its environment to survive. Animals, or other organisms, with the best models, have an advantage. For example, a cat pursuing mice will starve if it cannot predict their actions and behaviour. Conversely, the mouse needs a model of the dangers in its environment, including cats and their tendency to eat mice. The animal with the most effective modelling is likely to survive.
In order to open a lock, a key has a model of the lock. In this case, a key’s shape matches the mechanism to lift pins in the lock. In order to control (i.e. open or close) the lock the key must be a good match. The key is not the same as the lock. Its model is a shape that matches just the essential part of the lock’s geometry. Similarly, a locksmith picking the lock uses tools to lift the pins in the required pattern. The locksmith contains knowledge of how to open many such locks by matching and lifting the pins.

This managing system has a logical model that may have a completely different form from the regulated system. For example, a computer controlling a chemical plant does not contain an actual plant but a representation of the necessary inputs, interactions, and controls. Similarly, a neural network is an interconnected jumble. Your brain has an internal representation of that movie you watched, but how it formed, how it works, and its detailed location is obscure, to say the least. There is currently no satisfactory explanation of how the brain works.
This is a link to the original Ashby and Conant paper. It is a simplified account which is readable with a little effort. It was not intended as a technical tour de force but as an understandable presentation for people from various disciplines… Some AI people have questioned Ashby and Conant’s account (example) based on limited understanding. If you are one of this group, I suggest you reconsider the nature of Turing and Universal Turing Machines. Hint: the Universal Machine can model the Turing machine. Both machines produce the same output for a given input, and the Universal Machine does not need the same sequence of operations, just an equivalence (or model). Now generalise!