
Before we begin, this is about a great historical experiment. It says nothing about the efficacy and utility of vaccines. Don’t confuse science with technology: vaccination is a technology. We can accept Pasteur’s experiment on anthrax in sheep while understanding that it doesn’t apply elsewhere. Specifically, it doesn’t validate or invalidate any other vaccine, in any other disease, or any other animal. Just as a review of a Mercedes car does not apply to a Ducati motorcycle, despite both being forms of road transport conforming to Newton’s laws of motion. So here we are looking at a scientific experiment using 1880s technology. In other words, forget about politics and enjoy a remarkable trial.
The germ theory of disease and vaccination remains controversial, which was the case back in the late 19th century. Back then, anthrax was a scourge for French farmers. So Monsieur H. Rossignol demanded Pasteur do a public vaccine test at his farm in Pouilly-Le-Fort, a small village near Paris. For Pasteur, there was a considerable risk that failure would damage his reputation if the trial failed. I’m taking the initial account of the experiment from the CDC and The US National Library of Medicine here.
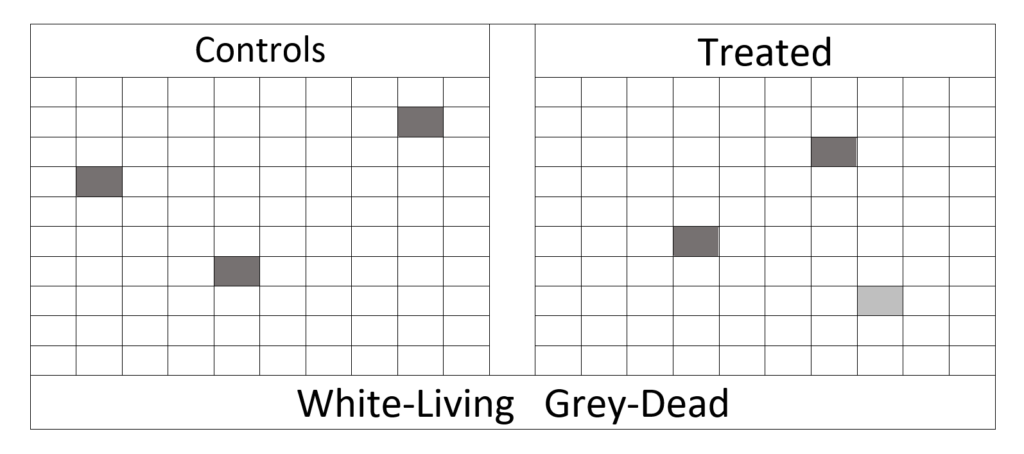
Pasteur vaccinated 25 sheep early in May. He had another 25 unvaccinated controls. At the end of the month, he gave all 50 a nasty form of anthrax. The fifty sheep remained together in the same cattle shed, being told apart by punching a hole in the ear of the vaccinated sheep. Witnesses arrived at the farm a few days later to view the results. The 25 vaccinated sheep were free of the disease, but all the controls had died.

This table is a graphical display of the results. The table represents sheep as cells. White is healthy, while grey is dead. Do you find this result convincing, or would you prefer some Evidence-Based Medicine (EBM)? Do we need a large-scale, well-designed, randomised, placebo-controlled, double-blind, blah blah clinical trial to be sure?
You would have good scientific judgement if you answered that we don’t need EBM. Indeed, the result is statistically definitive, but the experimental design might have had minor issues. For example, perhaps someone sneaked in and switched the sheep. Punching a hole in a treated sheep’s ear could have rendered it immune. These are unlikely scenarios, but this is the sort of argument that feeds Skeptics. In the real world, other scientists are supposed to resolve such issues by repeating the trial.
A wealthy landowner or vet wanting to check if this would work with his farms could bear the loss of 50 sheep. If funds were lacking, perhaps they could substitute some rabbits. In short, repeating the trial would be practical and relatively inexpensive. This experiment is powerful because it is small-scale and addresses a major problem.
Those large-scale blah blah trials cost millions and typically take years to complete. Few people have the resources to check the results without commercial or government funding. For some, this is a feature, not a bug. The medical industries saw an opportunity and organised to control medical research using EBM. The result is the recent chaos of SAR-COV-2, but this is outside the scope of this post.
Louis Pasteur
Louis Pasteur was brilliant but not a pleasant or trustworthy man. He misled everyone into thinking it was his vaccine used in the sheep trial. However, Pasteur did not have a treatment available and used one from a collaborator. He could always say that it wasn’t his vaccine if things went awry. Then after the trial’s success, he pushed ahead to get his vaccine working. The reasons for Pasteur’s actions are clear. He might become rich if he had a solution. New Scientist magazine reported, “there was big money to be made…Pasteur pushed aside a rival and got the government licence to produce the vaccine.”
Estimating the chances
There is some dispute about the details of Pasteur’s experiment. Pasteur’s write-up gives different numbers for the animals, for example. He was given 60 sheep but did not use 10 of them. The extra ten sheep acted as additional controls on the infection process.
Pasteur used ten bovines, eight cows, one bull and an ox; he vaccinated six and used the remaining four as controls. Unfortunately, these animals did not respond to anthrax or the vaccination to the same degree as the sheep. Also, Pasteur reports that he replaced two of the sheep with goats leaving 58 sheep.
Pasteur wrote, “The twenty-four sheep, the goat, and the six cows which had received the vaccinations of attenuated anthrax, all appeared healthy”. However, “twenty-one sheep and the goat which had
not been vaccinated had already died of anthrax; two other unvaccinated sheep died in front of the viewers, and the one remaining sheep died at the end of the day.” In addition, one vaccinated but pregnant sheep died the following day because the foetus had expired sometime before.
For simplicity, we will use the CDC account with 25 sheep in each group – 24 or 25 does not make a difference in the decision-making. We will use an online binomial calculator that estimates binary outcomes, in this case, dead or alive. I used Wolfram Alpha binomial probability calculator, but there are several others. So if you want to check, feel free to pick a more user-friendly one you prefer. There are several approaches to analysing the trial, so let’s take a simple example.
There were 25 control sheep, and none survived. From this, I can estimate the odds of an unvaccinated sheep’s death is about 975 in 1000 (p=0.975). With this probability value in the calculator, there is a 50% chance of getting no survivors in the 25 control sheep. We expect to get a single survivor 35% of the time, and so on. This estimate is consistent with Pasteur’s result and a reasonable approximation. While this approach seems conservative, make your own estimate if you have doubts. The results will be similar.
Putting p=0.975 into the calculator for the treated is interesting. The probability of getting no deaths is 6×10-40. That’s p=0.0000…000006 with 40 zeros; in other words, the chance this result is a statistical fluke is about zero, zilch, nada. Moreover, this result is definitive and easy to check. The people witnessing Pasteur’s experiment were able to recognise a breakthrough when they saw it.
Now the modern standards in EBM are significant, with one chance in 20 (p<=0.05), or highly significant, with odds of 1 in 100 (p<=0.01). So we might say the criteria in medical experimentation have degraded since the 1880s.
Modern Medicine
Let’s take statin study from modern medical science. The American Journal of Cardiology described statins as miracle drugs. They are to heart disease what “what penicillin was to infectious disease”. Doctors were urged to “convince patients that these miracle drugs…are the best anti-atherosclerotic insurance they can purchase.” So let’s see how these miracle drugs stack up to Pasteur.
I took the first meta-analysis that appeared in a google search. For those impressed with such things, the study was in a respected journal, JAMA (Journal of the American Medical Association). It has been peer-reviewed, passed the editor’s scrutiny, and all that jazz.
The study has all the EBM bells and whistles. It is large-scale “seventeen studies (21,303 patients) were included”. Their analysis “suggested that a meta-analysis sample size in the range of 20,000 patients would be required to achieve at least 80% power”. And so on with the waffle. All this waffle means is the study is no good. Pasteur didn’t bother with this stuff, but he wanted a worthwhile result. Either his treatment saved sheep, or it didn’t. In earlier days, people were more discerning and educational standards were high.
So the all-cause mortality was reported as 493 deaths in the statin-treated and 639 in the controls. They claim this means a 24% reduction by taking statins. In their words, “the OR [odds ratio] was 0.76 (95% confidence interval [CI], 0.67-0.86) in favor of receiving statin treatment”. This claim would please the drug companies. Wow, take our expensive statins; they really help you stay alive! Or do they?
We can calculate the risk to a control patient as 639/21,203 = 0.03 or 3%. Correspondingly, the risk to a statin-treated patient was 493/21,203 = 0.023 or 2.3%. So the actual benefit to a patient is 3%-2.3% = 0.7%. The paper magnified the actual benefit about 34 times. I suppose misleading people like this is good marketing for corporate medicine.
Not quite convinced? Let’s look at our table graphic as with Pasteur.
So look at the table. Do you find the statin benefit convincing? Put it another way. Would you spend $1,000 a year for the rest of your life to gain this benefit? Look carefully. The advantage gained is only a 0.7% reduction in risk. To achieve this possible benefit in one person, they will need to put 100 people on statins. That would mean the drug company received $100,000 yearly from the 100 patients.
Is there anything else you could do with the money? Do you think spending $1,000 yearly on supplements, gym membership, or more healthy food would help you more? What about taking a holiday or long walks in the woods? There are many other options. Consider the opportunity cost of spending this money on statins.

Pasteur’s result was definitive and needed. The farmers and sheep had a clear benefit, and the intervention was cheap. That’s why people remember it decades later. Conversely, the EBM result with statins is marketing. They want you to buy expensive drugs and interventions for their bottom line. Corporate medicine is massively profitable. The reason for all those large-scale blah blah blah trials is to hide the fact that they find it harder and harder to generate effective treatments. Make the clinical trials expensive enough, and only drug companies can afford them. Medicine is a corporate monopoly.
